For too long this blog has blundered around in theoretical la-la land. It’s time to get practical. Should you run if it starts raining?

An astonishing number of people have addressed the issue:
http://mathforum.org/library/drmath/view/63759.html
http://www.dctech.com/physics/features/0500.php
http://everything2.com/title/Is+it+better+to+run+or+walk+in+the+rain%253F
http://news.bbc.co.uk/2/hi/uk_news/magazine/4562132.stm
Including this one, which I only found after. :( http://www.dctech.com/physics/features/0600.php
ACCEPTED WISDOM
The theory everyone agrees on is that if it starts raining, you should start running.
How do they figure it out?
Everyone models it as two rectangles. A horizontal one that will get wet more the longer you are outside. A vertical one that will get wet the same no matter what.
This may work if you are built like a wardrobe. Or if you are Sponge Bob Squarepants.
MY THEORY
People are a jumble of angles when they run. I started thinking about the various angles and which raindrops would hit them if they were moving in the rain. I was sure it would be easy.
I started by drawing a picture of a raindrop.
Then I googled triangles; I got a pencil and paper; I went to maths for kids; I went to maths is fun; I got patronised; I got confused; I got another sheet of paper; I was reminded of my old nemeses, sine cos and tan; I rang my friend who has a degree in maths; I got out another sheet of paper, I am humbled to admit I used wolfram alpha, I used google; I learned the formula for the area of a trapezium; I got even more confused, I learned the definition of ‘radian’. I swore and went for a walk; I came back and did some more algebra.
I ended up with this:
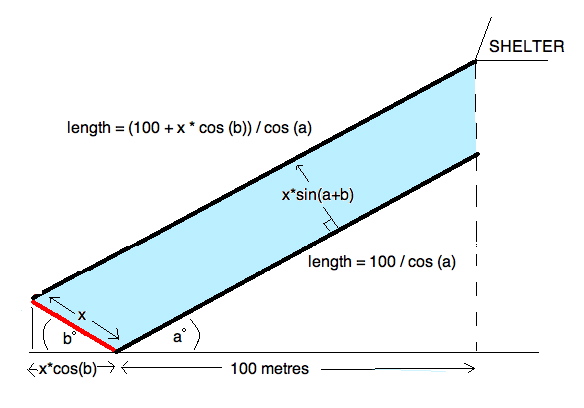 The red line represents a surface of your body, maybe your forearm. It is at an angle to the rain, (which we assume is falling straight down). The raindrops that fall on it are in the shaded area. The size of the shaded area depends on the angle of that surface (b), and on on angle (a).
The red line represents a surface of your body, maybe your forearm. It is at an angle to the rain, (which we assume is falling straight down). The raindrops that fall on it are in the shaded area. The size of the shaded area depends on the angle of that surface (b), and on on angle (a).
Angle a depends on how fast you are going. If you stand still, angle (a) will be 90 degrees, the shaded rectangle will be infinitely large, and you will get soaked. If you go across at the same speed the rain is falling down, angle a will be 45 degrees. [a=atan(ratio of rainspeed to personspeed)]
Here it gets interesting. A 45 degree forward angled slope, if it is traveling at the exact same speed across as the rain falls down, can theoretically move through the rain without getting wet!

If a + b =180, the surface will only be hit by raindrops that lie along the line! This is a lot less rain. There’s a neat formula for this. If you are going at the speed of the rain, you need to be on a gradient of 1. But if you are travelling at one fifth the speed of the rain, you need a gradient of 5 (79 deg) to stay most dry. A third the speed? You should lean forward til you are on a gradient of 3 .
Would a running person be about that shape?
I measured the angles on this running dude:
 .
.
I opened excel and faffed around.
Here’s one formula i had to use:
=IF(C60=6;((C59*(SIN((C57–C58)/(180/PI())))*((100/(COS((C57)/(180/PI())))+((100+(C59)*(COS((C58)/(180/PI())))/(COS((C57)/(180/PI())))/2))*C61*C62*C63))));0)
Ouch. I made sure I weighted each surface for how long each surface was exposed to the rain.
Here’s the results:
If he went 100 m through medium rain (falling at 5m/s), he would be hit by 601 raindrops running (at 4m/s), and 892 raindrops walking (1.4 m/s). That’s 48% more if he walks.
(However, running might be less comfortable, as he gets hit by three times as many raindrops every second! The difference is, he gets to shelter 46 seconds quicker.)
If he went through heavy rain (falling at 9m/s) he would be hit by 821 raindrops running, and 1290 walking. Walking is 57% wetter .
If he went through light rain (falling at 2 m/s) he would be hit by 633 drops while walking, and 462 running. (37% wetter walking)
Even walking head-on into 45 degree angled rain, you’re still about 30% drier if you run!
**UPDATE**
Dave suggested that if it’s windy, running away from the rain is the answer. He’s right:
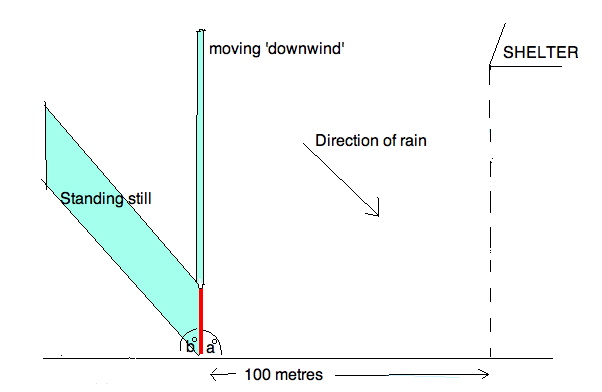 The calculations say that if you run downwind in medium rain, you get hit by 486 drops walking, and 137 drops running.
The calculations say that if you run downwind in medium rain, you get hit by 486 drops walking, and 137 drops running.
So, what have I shown?
1. Human intuition is right! Run when it rains.
2. The ‘spongebob model’ is a fair approximation. Adding in all the angles did not materially change the result.
3. Tip forward into the rain to cut down your exposure. The harder the rain, the more you need to tip. Maybe one of these dorktastic contraptions would help?
[picapp src=”f/f/b/9/FILE_PHOTO_dd2a.jpg?adImageId=6155950&imageId=2951327″ width=”170″ height=”297″ /]
4. Or one of these:

P.S. If anyone would like to access the spreadsheet I used, just say so in the comments below, and I can pass it to you for your use. :)
Mythbusters have also proved this but with a more practical (and ultimately more understandable) approach.
But I enjoyed the descriptions (and mental image) of your struggle with spreadsheets and various mathematical operators so that I suggest a weekly article demystifying science for all us plebs. Gravity, anyone?
LikeLike
I think you should look at cycling in the rain taking into account water splashed up from the ground and water falling from the sky. Is it better to cycle quickly (like running) knowing you will get more puddle spash, or go slow( the cycle walk) and be out there longer. The position of the cyclist would be the same.
Put that in your Excel pipe and smoke it!
Or get mud guards for your bike – bike snob would not approve!
LikeLike
actually the bike snob is the world’s biggest ‘wheel-brow’ advocate!
http://bikesnobnyc.blogspot.com/2009/05/indignity-of-commuting-by-bicycle_12.html
LikeLike
I agree with your theory. I would like to add the following concept…
If rain comes down vertically, this means there is nil wind. You will find there is only a vertical speed of rain. If you’re a flat panel on the ground, then the faster you move, the less wet you get.
If you introduce wind, then you get angled rain.
The rain still has the same mass, but part of its trajectory is now horizontal. If you consider 45 degree angle rain, you can derive that its vertical speed has been halved.
SO, if you (the flat panel) run downwind at the same horizontal speed of the rain you’ll find that you’re only exposed to the vertical speed of the rain mass. Thus seeing much less rain.
My theory is that if you want to run for shelter, you should always run downwind when possible.
LikeLike
dave you are totally right. I’m going to update this post with some pictures and run the model again to show the benefit of going downwind…
LikeLike
No running from this:
LikeLike
What a tool
LikeLike